Empat Pilar – Pengertian Kuartil dan Rumusnya : Dilengkapi Contoh soal. Apakah kamu pernah mendengar istilah kuartil dalam pelajaran matematika atau statistika dan bertanya-tanya apa sebenarnya itu?
Jangan khawatir, dalam artikel ini, kita akan membahas Pengertian Kuartil dan Rumusnya sampai tuntas! Tapi sebelum itu, mari kita pahami terlebih dahulu apa itu statistika.
Statistika adalah ilmu yang mempelajari pengumpulan, analisis, interpretasi, presentasi, dan organisasi data.
Dalam bekerja dengan data, kita sering kali menggunakan berbagai metode untuk memahami tren dan pola dalam data tersebut. Salah satu metode tersebut adalah kuartil.
Kuartil adalah sebuah metode dalam statistika yang digunakan untuk membagi suatu set data menjadi empat bagian sama besar.
Ini adalah bentuk dari kuantil, yang merupakan alat yang digunakan untuk membagi data. Jadi, Pengertian Kuartil dan Rumusnya adalah sebuah konsep penting dalam dunia statistika.
Pengertian Kuartil
Pengertian Kuartil dan Rumusnya, Kuartil atau yang dalam bahasa Inggris disebut Quartile, adalah nilai yang membagi kumpulan data yang terurut menjadi empat bagian yang sama. Terdapat tiga kuartil yang ditemukan dalam sebuah set data, yaitu Kuartil 1 (Q1), Kuartil 2 (Q2) atau Median, dan Kuartil 3 (Q3).
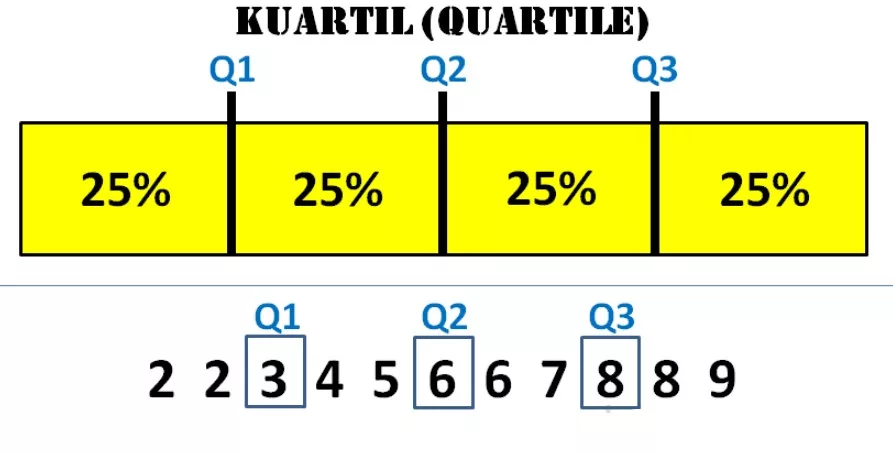
Dalam gambar di atas, terlihat dengan jelas bahwa terdapat empat bagian yang sama dalam kumpulan data yang dibagi berdasarkan kuartil, yaitu:
- 25% pertama merupakan bagian terendah.
- Bagian berikutnya sebesar 25% adalah bagian kedua, mulai dari bagian terendah hingga mencapai Median.
- Bagian setelah Median sebesar 25% adalah bagian tertinggi kedua.
- 25% terakhir merupakan bagian tertinggi.
Dengan menggunakan konsep kuartil ini, kita dapat memahami distribusi data yang lebih baik dan melihat bagaimana data terbagi secara proporsional.
Pengertian Kuartil Menurut Para Ahli
Masih dalam pembahasan Pengertian Kuartil dan Rumusnya, selanjutnya kuartil menurut para ahli adalah nilai-nilai yang digunakan untuk membagi serangkaian data atau distribusi frekuensi menjadi empat bagian yang sama. Konsep ini telah dijelaskan oleh beberapa ahli sebagai berikut:
- Wirawan (2001:105) menjelaskan bahwa kuartil (K) adalah nilai-nilai yang membagi serangkaian data atau distribusi frekuensi menjadi empat bagian yang sama. Dalam hal ini terdapat tiga kuartil, yaitu kuartil pertama (K1), kuartil kedua (K2), dan kuartil ketiga (K3).
- Suliyanto (2002:106) mendefinisikan kuartil sebagai pembagian kelompok data menjadi empat bagian, mulai dari bagian pertama hingga bagian keempat.
- Sudijono (2006:112) mengungkapkan bahwa kuartil adalah titik atau skor nilai yang membagi seluruh distribusi frekuensi menjadi empat bagian yang sama besar, masing-masing sebesar 1/4N. Dengan demikian, terdapat tiga kuartil, yaitu kuartil pertama (K1), kuartil kedua (K2), dan kuartil ketiga (K3).
Dalam pengertian yang diberikan oleh para ahli tersebut, kuartil digunakan untuk membagi data menjadi empat bagian yang memiliki ukuran yang sama.
Hal ini berguna dalam analisis statistik untuk mendapatkan pemahaman yang lebih baik tentang distribusi data dan mengidentifikasi posisi relatif suatu nilai dalam data tersebut.
Cara Mencari Kuartil Data Tunggal
Dari penjelasan sebelumnya mengenai kuartil, dapat disimpulkan bahwa kuartil adalah proses pembagian data menjadi empat bagian dengan jumlah yang sama. Oleh karena itu, terdapat tiga nilai kuartil yang digunakan untuk membagi data tersebut.
Sebelum melakukan pembagian data, langkah pertama yang perlu dilakukan adalah mengurutkan data secara terlebih dahulu.
Untuk memperoleh pemahaman yang lebih jelas, gambar di bawah ini dapat digunakan sebagai referensi.
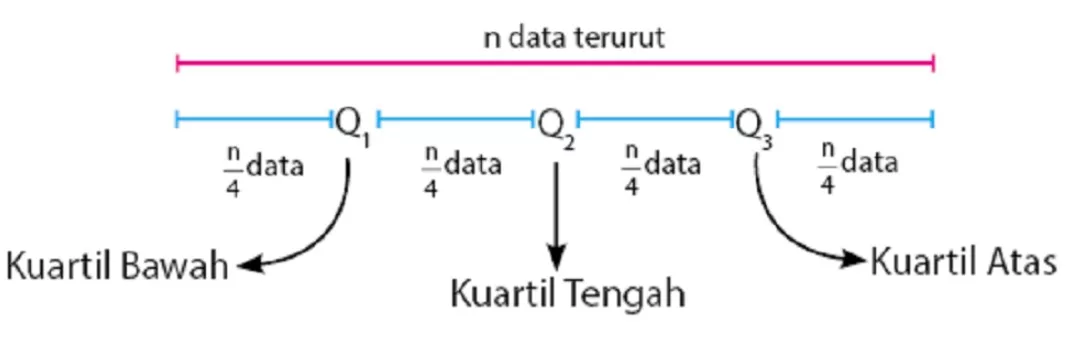
Ketika mencari nilai kuartil untuk data tunggal, terdapat dua rumus yang berbeda, tergantung pada jumlah data yang ada, baik itu ganjil atau genap.
1. Untuk Mencari n ganjil :

2. Untuk mencari n genap :
Tahapan dalam mencari tiga nilai kuartil untuk data tunggal dengan jumlah data genap adalah sebagai berikut:
- Carilah nilai yang menjadi median (Q2) dari data tersebut.
- Bagi data di sebelah kiri median menjadi dua bagian yang sama dan temukan nilai yang menjadi kuartil bawah (Q1).
- Bagi data di sebelah kanan median menjadi dua bagian yang sama dan temukan nilai yang menjadi kuartil atas (Q3).
Dengan mengikuti tahapan tersebut, kita dapat menemukan nilai Q1, Q2 (median), dan Q3 untuk data tunggal dengan jumlah data genap.
Rumus Kuartil Data Tunggal
Rumus-rumus untuk menghitung nilai kuartil pada data tunggal adalah sebagai berikut:
1. Kuartil Bawah (Q1) dapat dihitung dengan rumus:
Q1 = ¼ (n+1)
Dalam rumus tersebut, n merupakan jumlah data dalam himpunan data tunggal. Untuk mencari nilai Q1, kita mengalikan ¼ dengan jumlah data yang ditambah satu (n+1).
2. Kuartil Tengah (Q2) atau median dapat dihitung dengan rumus:
Q2 = ½ (n+1)
Dalam rumus ini, juga menggunakan jumlah data dalam himpunan data tunggal (n). Untuk menemukan nilai Q2, kita mengalikan ½ dengan jumlah data yang ditambah satu (n+1).
3. Kuartil Atas (Q3) dapat dihitung dengan rumus:
Q3 = ¾ (n+1)
Rumus ini juga menggunakan jumlah data dalam himpunan data tunggal (n). Untuk mencari nilai Q3, kita mengalikan ¾ dengan jumlah data yang ditambah satu (n+1).
Dengan menggunakan rumus-rumus tersebut, kita dapat menghitung nilai kuartil (Q1, Q2, dan Q3) pada data tunggal dengan mudah dan akurat.
A. Contoh Cara Mencari Kuartil Data Tunggal
Berikut ini adalah perhitungan dan contoh soal atau contoh kasus untuk mencari Kuartil Data Tunggal.
1. Kuartil data tunggal dengan jumlah data ganjil
Terdapat sejumlah data pengujian yang terdiri dari 5, 7, 4, 4, 6, 2, 8. Cari nilai Q1, Q2, dan Q3.
Langkah 1: Urutkan data menjadi 2, 4, 4, 5, 6, 7, 8.
Langkah 2: Cari Q1, Q2, dan Q3 berdasarkan rumus Kuartil data tunggal.
Q1 = ¼ (n+1)
Q1 = ¼ (7+1)
Q1 = ¼ (8)
Q1 = 2
Dengan demikian, Q1 berada di posisi ke-2, yaitu angka 4.
Q2 = ½ (n+1)
Q2 = ½ (7+1)
Q2 = ½ (8)
Q2 = 4
Dengan demikian, Q2 berada di posisi ke-4, yaitu angka 5.
Q3 = ¾ (n+1)
Q3 = ¾ (7+1)
Q3 = ¾ (8)
Q3 = 6
Dengan demikian, Q3 berada di posisi ke-6, yaitu angka 7.
2. Kuartil data tunggal dengan jumlah data genap
Hitunglah Q1, Q2, dan Q3 dari data berikut ini: 1, 3, 3, 4, 5, 6, 6, 7.
Langkah 1: Urutkan data menjadi 1, 3, 3, 4, 5, 6, 6, 7.
Langkah 2: Cari Q1, Q2, dan Q3 berdasarkan rumus Kuartil data tunggal.
Q1 = ¼ (n+1)
Q1 = ¼ (8+1)
Q1 = ¼ (9)
Q1 = 2,25 → Posisi di antara 2 dan 3.
Karena berada di antara 2 dan 3, maka kita harus menghitung rata-rata dari angka yang berada di posisi 2 dan 3 tersebut, yaitu (3+3)/2 = 3.
Q2 = ½ (n+1)
Q2 = ½ (8+1)
Q2 = ½ (9)
Q2 = 4,5 → Posisi di antara 4 dan 5.
Karena berada di antara 4 dan 5, maka Q2 adalah nilai yang tepat, yaitu 4,5.
Q3 = ¾ (n+1)
Q3 = ¾ (8+1)
Q3 = ¾ (9)
Q3 = 6,75 → Posisi di antara 6 dan 7.
Karena berada di antara 6 dan 7, maka kita harus menghitung rata-rata dari angka yang berada di posisi 6 dan 7 tersebut, yaitu (6+6)/2 = 6.
B. Cara Mencari Kuartil Data Kelompok
Selain Pengertian Kuartil dan Rumusnya, Nah ada data kelompok adalah data yang dikelompokkan berdasarkan kelompok pengukuran atau kategori yang sama dan umumnya disajikan dalam bentuk tabel atau histogram.
Untuk menghitung Kuartil Data Kelompok, kita perlu menggunakan rumus khusus.
1. Rumus Kuartil Data Kelompok
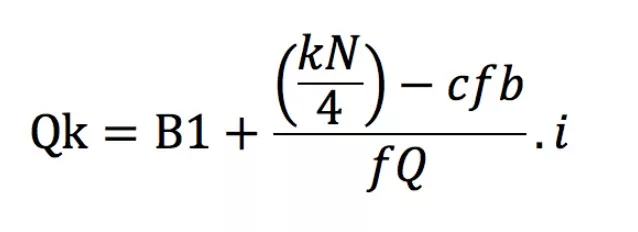
Qk = Kuartil ke k
B1 = Batas bawah nyata dari kelas yang berisi Qk
cfb = Frekuensi Kumulatif di bawah kelas yang berisi Qk
fQ = Frekuensi kelas yang berisi Qk
i = interval kelas
k = 1, 2, 3 (Kuartil yang ingin dihitung)
N = jumlah observasi
Dalam rumus ini, kita akan menggunakan frekuensi kumulatif (cf) dan frekuensi kelas (f) untuk menemukan batas bawah nyata kelas (B1) yang mengandung kuartil yang ingin dihitung.
2. Contoh Cara Mencari Kuartil pada Data Kelompok
Sebuah perusahaan sedang melakukan penelitian tentang hasil penjualan dari 20 karyawan pemasarannya. Berikut adalah data yang diperoleh oleh perusahaan tersebut dalam tabel di bawah ini:
| Penjualan (Rp dalam Juta) | Frekuensi |
|---|---|
| 8 – 10 | 2 |
| 11 – 13 | 4 |
| 14 – 16 | 6 |
| 17 – 19 | 4 |
| 20 -22 | 3 |
| 23 -25 | 1 |
| Banyaknya Observasi | 20 |
Penyelesaian:
- Langkah pertama adalah menghitung Frekuensi Kumulatif (fQ) dengan hasil seperti yang terlihat pada tabel di bawah ini:
| Penjualan (Rp dalam Juta) | Frekuensi | Frekuensi Kumulatif |
| 8 – 10 | 2 | 2 |
| 11 – 13 | 4 | 6 |
| 14 – 16 | 6 | 12 |
| 17 – 19 | 4 | 16 |
| 20 -22 | 3 | 19 |
| 23 -25 | 1 | 20 |
| Banyaknya Observasi | 20 |
- Langkah kedua adalah mencari posisi Kuartil yang diinginkan. Dalam contoh ini, kita akan mencari Kuartil Kedua atau Q2. Menggunakan rumus data tunggal, kita mendapatkan hasil Q2 berada di posisi 10,5, yaitu di kelas [13,5 – 16,5].
Berikut adalah cara untuk mencari Q2:
Q2 = ½ (n+1)
Q2 = ½ (20+1)
Q2 = ½ (21)
Q2 = 10,5
- Langkah ketiga atau langkah selanjutnya adalah mencari Kuartil Kedua Q2 Data Kelompok dengan menggunakan rumus Kuartil Data Kelompok di atas.
Diketahui:
Qk = 2
B1 = 13
cfb = 6
fQ = 6
i = 3
k = 2
N = 20
Jawaban:
Jadi, Kuartil 2 atau Q2 dari data di atas adalah 15.
Kesimpulan
Demikianlah artikel dari empatpilar.com ini mengupas tuntas mengenai Pengertian Kuartil dan Rumusnya, dan contoh soal sebagai ilustrasi dalam pengaplikasiannya. Semoga pengetahuan ini menjadi tambahan bagi kita semua dalam memahami konsep statistik ini.
Ingatlah bahwa memahami kuartil tidak hanya berarti menghafal rumusnya, tetapi juga mengetahui bagaimana menggunakannya dengan tepat dan efektif dalam analisis data.
Setiap angka dalam kuartil menggambarkan informasi penting tentang data kita, dan penggunaan yang tepat akan membantu kita membuat keputusan yang lebih baik berdasarkan data tersebut.
Tidak ada akhir untuk pembelajaran, dan kuartil hanyalah salah satu bagian dari dunia statistik yang luas dan kompleks.
Semoga dengan memahami Pengertian Kuartil dan Rumusnya, Kalian semakin bersemangat untuk terus belajar dan mengeksplorasi lebih dalam tentang statistik. Akhir kata, teruslah belajar dan berkreasi! Kata Pencarian Terpopulerpenjelasan dan rumus kuartil